APPLICATION OF GAUSSIAN PROCESS REGRESSION METHOD TO GUST FORECASTING IN WINTER AND SPRING IN ZHEJIANG COASTAL ISLANDS
-
摘要: 利用2006—2016年冬春季浙江四个海岛气象站10 m大风观测资料和ERA-interim资料，首先分析了阵风因子和阵风风速的概率分布特征；然后统计阵风与10 m至500 hPa层的气温、风速、散度、涡度、比湿、垂直速度、浮力能等要素的关系，选取高相关的预报因子；最后采用高斯过程回归方法建立阵风概率预报模型，并进行试报。(1)平均风速相同时对应的阵风因子变化较大，导致阵风也出现大的差异，说明阵风数据分布具有混沌性；阵风风速具有正态或准正态分布特点，在自然对数处理后完全符合正态分布，表明采用高斯过程回归方法建立阵风概率预报模型合理可行。(2)阵风与大气低层的动力因子相关较好，而在近中层则与热力因子相关较好。(3)阵风大值样本在大气低层具有更强的下沉速度，有利于上层动量向下输送，且大值样本对应的中层气温和比湿相对大些，说明中层暖湿气流有利于湍流的发展和不稳定能量的交换。(4)试报模型的因子权重尺度分析表明，最佳预报因子绝大多数集中在875 hPa层以下，说明大气低层因子对近地面阵风起主导作用。(5)高斯过程回归模型试报表明，大部分站点阵风预报的50%概率区间上下界跨度约为2.5 m/s，75%概率区间跨度约为4.5 m/s，样本的50%和75%概率区间击中率均符合预期。Abstract: By the use of the gale data and ERA-interim data from four island meteorological stations in Zhejiang during winter and spring from 2006 to 2016, the climatic probability distribution characteristics of gust factors and gust velocity are analyzed first. Then the relationship between gust and meteorological factors such as temperature, wind speed, divergence, vorticity, specific humidity, vertical velocity and buoyancy energy from 500 hPa to the ground level are statistically analyzed. Finally, the Gaussian process regression method is used to establish a probability forecast model of gust, and the trial and comparison analysis are made. The following conclusions are drawn. (1) When the average wind speed is the same, the corresponding gust factors can change greatly, which leads to the big difference of gust, indicating that there is chaos in gust data distribution. Coastal gust wind speed has normal or quasi-normal distribution characteristics, which fully conforms to normal distribution after natural logarithm processing. Gust data characteristics show that the probability prediction method based on Gaussian process regression is reasonable and feasible. (2) Gust has a good correlation with the dynamic factors in the lower atmospheric layer, whereas it has a good correlation with the thermodynamic factors in the near middle atmospheric layer. (3) The sinking velocity of large gust samples is stronger in the lower layer, which is conducive to the downward transport of momentum in the upper layer. Moreover, the temperature and humidity in the middle layer are relatively higher, which indicates that the warm and humid air flow in the middle layer is more conducive to the turbulent development and the exchange of unstable energy. (4) Weight scale analysis of sample tests shows that most of the selected predictors are concentrated below 875hPa layer, indicating that the lower atmosphere factors play a dominant role in gust near surface. (5) The test results of Gaussian process regression model show that the 75% probability forecast interval span of samples at most stations is about 4.5 m/s, and the 50% probability forecast interval span is about 2.5 m/s. The 50% and 75% probability interval hit rates of samples are in line with expectations.
-
Key words:
- Gaussian process regression /
- coast /
- gust /
- probability /
- forecast
-
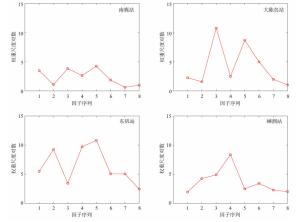
图 5 四个气象站阵风预报模型中8个因子对应的权重尺度对数情况
1：d875；2：w975；3：q500；4：t600；5：w600；6：b700_1000；7：f925；8：f1000, 要素说明同表 1。
表 1 各站不同天气要素与阵风相关检验的p值均值在0.05以下的因子 f：水平风速；t：气温；v：涡度；w：垂直速度；d：散度；q：比湿；b：浮力能。
试验 w500 q500 w500 q550 t600 w600 q600 t650 w650 q650 t700 嵊泗 0.01 0.00 0.03 0.01 0.00 0.08 0.02 0.00 0.13 0.02 0.02 南麂 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 大陈岛 0.02 0.00 0.00 0.00 0.00 0.00 0.00 0.01 0.00 0.00 0.05 东矶 0.00 0.00 0.00 0.00 0.04 0.00 0.00 0.01 0.00 0.02 0.07 平均 0.01 0.00 0.01 0.00 0.01 0.02 0.00 0.00 0.03 0.01 0.03 试验 q700 d750 d775 f850 f870 d875 f900 f925 w925 w950 f950 嵊泗 0.03 0.01 0.06 0.00 0.00 0.00 0.00 0.00 0.11 0.11 0.00 南麂 0.00 0.00 0.00 0.00 0.18 0.02 0.01 0.00 0.00 0.00 0.01 大陈岛 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 东矶 0.15 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 平均 0.04 0.00 0.02 0.00 0.05 0.01 0.00 0.00 0.03 0.03 0.00 试验 f970 d975 v975 w975 w1000 f1000 b600_1000 b700_1000 f10m 南麂 0.00 0.13 0.00 0.12 0.01 0.00 0.00 0.00 0.00 嵊泗 0.01 0.00 0.08 0.00 0.00 0.01 0.00 0.00 0.00 大陈岛 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 东矶 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 平均 0.00 0.03 0.02 0.03 0.00 0.00 0.00 0.00 0.00 
下载: 导出CSV
表 2 准因子之间相关检验p值的平均 要素说明同表 1。
要素 q500 w500 w550 q550 t600 w600 q600 t650 w650 p平均值 0.05 0.04 0.04 0.04 0.07 0.05 0.04 0.06 0.04 要素 q650 q700 t700 d750 d775 f850 f870 d875 f900 p平均值 0.02 0.02 0.03 0.04 0.04 0.06 0.08 0.11 0.13 要素 f925 w925 w950 f950 f970 v975 w975 d975 w1000 p平均值 0.14 0.01 0.02 0.04 0.02 0.10 0.03 0.05 0.02 要素 f1000 f10m b600_1000 b700_1000 p平均值 0.06 0.05 0.07 0.08
下载: 导出CSV
表 3 四个站点前10个阵风风速最大样本的入选因子平均值情况 要素说明同表 1。
站号 10 m阵风/(m/s) d875/(10-6·s-1) f925/(m/s) f1000/(m/s) q500 t600/K w600/(Pa/s) w975/(Pa/s) b700_1000/（m2/s2） 东矶 23.4 -11.1 17.2 15.4 0.001 4 267.8 -0.311 0.231 220.1 南麂 27.7 -18.5 14.5 16.2 0.002 1 269.4 -0.216 0.113 234.8 嵊泗 25.6 -10.9 19.5 17.2 0.001 4 267.8 -0.136 0.005 209.9 大陈岛 24.9 -15.9 17.8 17.3 0.001 7 268.2 -0.319 0.192 224.6 平均 25.4 -14.1 17.2 16.5 0.001 6 268.3 -0.245 0.135 222.3
下载: 导出CSV
表 4 四个站点10个阵风风速为10.1 m/s小值样本的入选因子平均值情况 要素说明同表 1。
站号 10 m阵风/(m/s) d875/(10-6·s-1) f925/(m/s) f1000/(m/s) q500 t600/K w600/(Pa/s) w975/(Pa/s) b700_1000/（m2/s2） 东矶 10.1 -7.60 5.5 6.1 0.000 7 267.8 -0.018 -0.008 200.6 南麂 10.1 -2.54 4.2 6.5 0.001 4 267.8 -0.064 -0.006 192.6 嵊泗 10.1 2.49 7.6 7.6 0.000 7 264.6 0.012 0.029 185.6 大陈岛 10.1 -5.53 6.4 7.5 0.001 0 266.2 0.047 0.083 202.9 平均 10.1 -3.29 5.9 6.9 0.000 9 266.6 -0.005 7 0.024 195.4
下载: 导出CSV
表 5 四个站点预报模型的拟合和测试结果
站号 拟合样本绝对误差/（m/s） 测试样本绝对误差/（m/s） 75%概率区间上下界差/（m/s） 50%概率区间上下界差/（m/s） 75%概率击中率/% 50%概率击中率/% 东矶 1.6 1.6 4.5 2.6 75.1 49.5 南麂 1.7 1.8 5.3 3.1 75.4 53.4 嵊泗 1.4 1.5 4.5 2.6 75.9 51.3 大陈岛 1.4 1.4 4.2 2.4 76.0 51.9 平均 1.5 1.5 4.6 2.6 75.6 51.2
下载: 导出CSV
-
[1] 王志春, 植石群.登陆台风启德近地层强风特性观测研究[J].气象科技, 2014, 42(4): 678-681. doi: 10.3969/j.issn.1671-6345.2014.04.026 [2] 宋丽莉, 毛慧琴, 汤海燕, 等.广东沿海近地层大风特性的观测分析[J].热带气象学报, 2004, 20(6): 731-736. doi: 10.3969/j.issn.1004-4965.2004.06.014 [3] 徐家良, 穆海振.台风影响下上海近海风场特性的数值模拟分析[J].热带气象学报, 2009, 25(3): 281-286. doi: 10.3969/j.issn.1004-4965.2009.03.004 [4] LARS M B, LARS R S. Wind gust factors in a coastal wind climate[C]//13th Deep Sea Offshore Wind R & D Conference, EERA Deep Wind, 20-22 January 2016, Trondheim, Norway. Energy Procedia 94(2016): 417-424. [5] NAKAMURA K, KERSHAW R, GAIT N. Prediction of near~surface gusts generated by deep convection[J]. Meteor Appl, 1996, 3(2):157-167. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=10.1002/met.5060030206 [6] BRADBURY W M S, DEAVES D M, HUNT J C R, et al. The importance of convective gusts[J]. Meteor Appl, 1994, 1(4): 365-378. http://www.researchgate.net/publication/229923194_the_importance_of_convective_gusts [7] BRASSEUR O. Development and application of a physical approach to estimating wind gusts[J]. Mon Wea Rev, 2001, 129(1): 5-25. doi: 10.1175/1520-0493(2001)129<0005:DAAOAP>2.0.CO;2 [8] 董双林.中国的阵风极值及其统计研究[J].气象学报, 2001, 59(3): 327-333. http://d.old.wanfangdata.com.cn/Periodical/qxxb200103007 [9] LORENZ E N.混沌的本质[M].刘式达, 刘式适, 严中伟译.北京: 气象出版社, 1997. [10] 丑纪范.大气科学中的非线性和复杂性[M].北京:气象出版社, 2002. [11] 杜钧, 陈静.单一值预报向概率预报转变的基础:谈谈集合预报及其带来的变革[J].气象, 2010, 36(11): 1-11. doi: 10.7519/j.issn.1000-0526.2010.11.001 [12] 杜钧, 邓国.单一值预报向概率预报转变的价值:谈谈概率预报的检验和应用[J].气象, 2010, 36(12): 10-18. doi: 10.7519/j.issn.1000-0526.2010.12.002 [13] 赵琳娜, 刘莹, 包红军, 等.基于重组降水集合预报的洪水概率预报[J].应用气象学报, 2017, 28(5): 544-554. http://d.old.wanfangdata.com.cn/Periodical/yyqxxb201705003 [14] MURPHY A H, MARTIN E. On the relationship between the accuracy and value of forecasts in the cost-loss ratio situation[J]. Wea Forecasting, 1987, 2(1): 243-251. http://www.researchgate.net/publication/249612528_On_the_Relationship_between_the_Accuracy_and_Value_of_Forecasts_in_the_Cost_Loss_Ratio_Situation [15] APPLEQUIST S, GAHRS G E, PFEFFER R L. Comparison of methodologies for probabilistic quantitative precipitation forecasting[J]. Wea Forecasting, 2002, 17(4): 783-799. doi: 10.1175/1520-0434(2002)017<0783:COMFPQ>2.0.CO;2 [16] KRZYSZTOFOWICZ R. Bayesian theory of probabilistic forecasting via deterministic hydrologic model[J]. Water Resour Res, 1999, 35(9): 2 739-2 750. doi: 10.1029/1999WR900099 [17] KALNAY E. Atmopsheric modeling, date assimilation and predictability[M]. Cambridge University Press, 2003. [18] 邓国, 龚建东, 邓莲堂, 等.国家级区域集合预报系统研发和性能检验[J], 应用气象学报, 2010, 21(5): 513-523. doi: 10.3969/j.issn.1001-7313.2010.05.001 [19] 刘家峻, 张立凤, 关吉平, 等.集合预报产品在台风麦莎预报中的应用[J].气象, 2010, 36(5): 21-31. http://d.old.wanfangdata.com.cn/Periodical/qx201005003 [20] 马培迎.应用贝叶斯原理修正降水概率预报[J].气象科技, 1999(1): 45-48. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=qxkj199901008 [21] 陈朝平, 马汉中, 陈静.基于贝叶斯方法的四川暴雨集合概率预报产品释用[J].气象, 2010, 35(5): 32-39. doi: 10.3969/j.issn.1003-6598.2010.05.012 [22] 邵明轩, 刘凤辉, 程维中, 等.用非线性多因子动态组合方法作降水概率预报[J].气象科技, 2003, 31(4): 206-210 doi: 10.3969/j.issn.1671-6345.2003.04.003 [23] 李明.基于ECMWF细网格模式的短时强降水客观概率预报方法研究[J].热带气象学报, 2017, 33(6): 812-821. http://www.itmm.org.cn/rdqxxb/ch/reader/view_abstract.aspx?file_no=20170602&flag=1 [24] 姜丽黎, 余晖.基于动力相似方法的台风极端降水概率预报研究[J].热带气象学报, 2019, 35(3): 353-364. http://www.itmm.org.cn/rdqxxb/ch/reader/view_abstract.aspx?file_no=20190308&flag=1 [25] SLOUGHTER J M, GNEITING T, RAFTERY A E. Probabilistic wind speed forecasting using ensembles and Bayesian model averaging[J]. J Amer Stat Assoc, 2010, 105(489): 25-35. doi: 10.1198/jasa.2009.ap08615 [26] LERCH S, THORARINSDOTTIR T L. Comparison of nonhomogeneous regression models for probabilistic wind speed forecasting[J]. Tellus, 2013, 65(10): 98-110 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=Arxiv000000932761 [27] THORARINSDOTTIR T L, JOHNSON M S. Probabilistic wind gust forecasting using nonhomogeneous Gaussian regression[J]. Mon Wea Rev, 2012, 140(3): 889-897. doi: 10.1175/MWR-D-11-00075.1 [28] HARPER B A, KEPERT J D, GINGER J D. Guidelines for converting between various wind averaging periods in tropical cyclone conditions[C]//Sixth Tropical Cyclone RSMCs. Brisbane: WCs Technical Coordination Meeting Technical Document, 2009. [29] 何志昆, 刘光斌, 赵曦晶, 等.高斯过程回归方法综述[J].控制与决策, 2013, 28(8): 1 121-1 137. http://d.old.wanfangdata.com.cn/Periodical/kzyjc201308001 [30] 王鑫, 李红丽.台风最大风速预测的高斯过程回归模型[J].计算机应用研究, 2015, 32(1): 59-62. doi: 10.3969/j.issn.1001-3695.2015.01.014 [31] 龙健颜, 卢素, 刘金山.贝叶斯非参数回归模型及非参数似不相关回归模型的应用[J].统计与决策, 2011, 27(16): 17-20. http://d.old.wanfangdata.com.cn/Periodical/tjyjc201116006 [32] KOTTAS A, BEHSETA S, MOORMAN D E, et al. Bayesian nonparametric analysis of neuronal intensity rates[J]. J Neuroscience Methods, 2012, 203(1):241-253. doi: 10.1016/j.jneumeth.2011.09.017 [33] 王磊, 邹北骥, 彭小宁, 等.基于高斯过程的表情动作单元跟踪技术[J].电子学报, 2007, 35(11): 2 087-2 091. doi: 10.3321/j.issn:0372-2112.2007.11.011 [34] FELDMANN K, SCHEUERER M, THORARINSDOTTIR T L. Spatial postprocessing of ensemble forecasts for temperature using nonhomogeneous gaussian regression[J]. Mon Wea Rev, 2015, 143(3):955-971. doi: 10.1175/MWR-D-14-00210.1 -
点击查看大图
图(7) / 表(5)
计量
- 文章访问数: 86
- HTML全文浏览量: 7
- PDF下载量: 41
- 被引次数: 0
